|
Je cherche à compiler la figure d'Alain Matthes sur le produit matriciel. Il y a une erreur à la compilation (je compile avec pdflatex sur miktex, tout vient d'être mis à jour) : ! Package pgf Error: No shape named A-2-1 is known. See the pgf package documentation for explanation. Type H <return> for immediate help. ... l.80 \draw[blue] (A-2-1.north) --(C-2-2.north); This error message was generated by an \errmessage command, so I can't give any explicit help. Pretend that you're Hercule Poirot: Examine all clues, and deduce the truth by order and method. ! Package pgf Error: No shape named C-2-2 is known. See the pgf package documentation for explanation. Type H <return> for immediate help. ... |
|
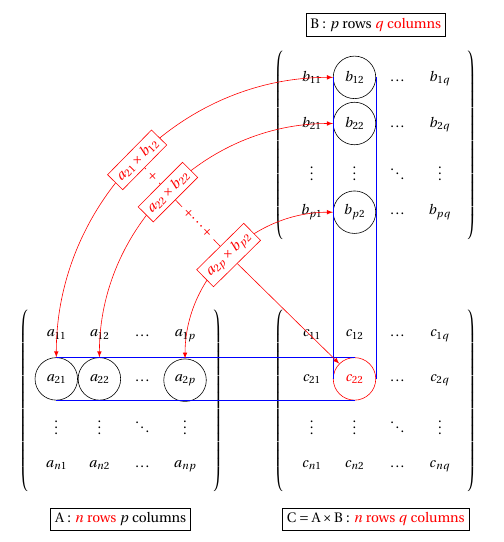
Les nœuds des matrices A, B et C ne sont pas nommés : il faut donc ajouter les noms (A-2-1), (A-2-2) etc. Voici le code complet : \documentclass[]{article} \usepackage[utf8]{inputenc} \usepackage[upright]{fourier} \usepackage{tikz} \usetikzlibrary{matrix,arrows,decorations.pathmorphing} \begin{document} % l' unite \newcommand{\myunit}{1 cm} \tikzset{ node style sp/.style={draw,circle,minimum size=\myunit}, node style ge/.style={circle,minimum size=\myunit}, arrow style mul/.style={draw,sloped,midway,fill=white}, arrow style plus/.style={midway,sloped,fill=white}, } \begin{tikzpicture}[>=latex] % les matrices \matrix (A) [matrix of math nodes,% nodes = {node style ge},% left delimiter = (,% right delimiter = )] at (0,0) {% a_{11} & a_{12} & \ldots & a_{1p} \\ \node[node style sp] (A-2-1) {a_{21}};% & \node[node style sp] (A-2-2) {a_{22}};% & \ldots% & \node[node style sp] (A-2-4) {a_{2p}}; \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \ldots & a_{np} \\ }; \node [draw,below=10pt] at (A.south) { $A$ : \textcolor{red}{$n$ rows} $p$ columns}; \matrix (B) [matrix of math nodes,% nodes = {node style ge},% left delimiter = (,% right delimiter =)] at (6*\myunit,6*\myunit) {% b_{11} & \node[node style sp] (B-1-2) {b_{12}};% & \ldots & b_{1q} \\ b_{21} & \node[node style sp] (B-2-2) {b_{22}};% & \ldots & b_{2q} \\ \vdots & \vdots & \ddots & \vdots \\ b_{p1} & \node[node style sp] (B-4-2) {b_{p2}};% & \ldots & b_{pq} \\ }; \node [draw,above=10pt] at (B.north) { $B$ : $p$ rows \textcolor{red}{$q$ columns}}; % matrice résultat \matrix (C) [matrix of math nodes,% nodes = {node style ge},% left delimiter = (,% right delimiter = )] at (6*\myunit,0) {% c_{11} & c_{12} & \ldots & c_{1q} \\ c_{21} & \node[node style sp,red] (C-2-2) {c_{22}};% & \ldots & c_{2q} \\ \vdots & \vdots & \ddots & \vdots \\ c_{n1} & c_{n2} & \ldots & c_{nq} \\ }; % les fleches \draw[blue] (A-2-1.north) -- (C-2-2.north); \draw[blue] (A-2-1.south) -- (C-2-2.south); \draw[blue] (B-1-2.west) -- (C-2-2.west); \draw[blue] (B-1-2.east) -- (C-2-2.east); \draw[<->,red](A-2-1) to[in=180,out=90] node[arrow style mul] (x) {$a_{21}\times b_{12}$} (B-1-2); \draw[<->,red](A-2-2) to[in=180,out=90] node[arrow style mul] (y) {$a_{22}\times b_{22}$} (B-2-2); \draw[<->,red](A-2-4) to[in=180,out=90] node[arrow style mul] (z) {$a_{2p}\times b_{p2}$} (B-4-2); \draw[red,->] (x) to node[arrow style plus] {$+$} (y)% to node[arrow style plus] {$+\raisebox{.5ex}{\ldots}+$} (z)% to (C-2-2.north west); \node [draw,below=10pt] at (C.south) {$ C=A\times B$ : \textcolor{red}{$n$ rows} \textcolor{red}{$q$ columns}}; \end{tikzpicture} \begin{tikzpicture}[>=latex] unit defintion of matrices \matrix (A) [matrix of math nodes,% nodes = {node style ge},% left delimiter = (,% right delimiter = )] at (0,0) {% a_{11} &\ldots & a_{1k} & \ldots & a_{1p} \\ \vdots & \ddots & \vdots & \vdots & \vdots \\ \node[node style sp] (A-3-1) {a_{i1}};& \ldots% & \node[node style sp] (A-3-3) {a_{ik}};% & \ldots% & \node[node style sp] (A-3-5) {a_{ip}}; \\ \vdots & \vdots& \vdots & \ddots & \vdots \\ a_{n1}& \ldots & a_{nk} & \ldots & a_{np} \\ }; \node [draw,below] at (A.south) { $A$ : \textcolor{red}{$n$ rows} $p$ columns}; \matrix (B) [matrix of math nodes,% nodes = {node style ge},% left delimiter = (,% right delimiter =)] at (7*\myunit,7*\myunit) {% b_{11} & \ldots& \node[node style sp] (B-1-3) {b_{1j}};% & \ldots & b_{1q} \\ \vdots& \ddots & \vdots & \vdots & \vdots \\ b_{k1} & \ldots& \node[node style sp] (B-3-3) {b_{kj}};% & \ldots & b_{kq} \\ \vdots& \vdots & \vdots & \ddots & \vdots \\ b_{p1} & \ldots& \node[node style sp] (B-5-3) {b_{pj}};% & \ldots & b_{pq} \\ }; \node [draw,above] at (B.north) { $B$ : $p$ rows \textcolor{red}{$q$ columns}}; % matrice resultat \matrix (C) [matrix of math nodes,% nodes = {node style ge},% left delimiter = (,% right delimiter = )] at (7*\myunit,0) {% c_{11} & \ldots& c_{1j} & \ldots & c_{1q} \\ \vdots& \ddots & \vdots & \vdots & \vdots \\ c_{i1}& \ldots & \node[node style sp,red] (C-3-3) {c_{ij}};% & \ldots & c_{iq} \\ \vdots& \vdots & \vdots & \ddots & \vdots \\ c_{n1}& \ldots & c_{nk} & \ldots & c_{nq} \\ }; \node [draw,below] at (C.south) {$ C=A\times B$ : \textcolor{red}{$n$ rows} \textcolor{red}{$q$ columns}}; % arrows \draw[blue] (A-3-1.north) -- (C-3-3.north); \draw[blue] (A-3-1.south) -- (C-3-3.south); \draw[blue] (B-1-3.west) -- (C-3-3.west); \draw[blue] (B-1-3.east) -- (C-3-3.east); \draw[<->,red](A-3-1) to[in=180,out=90] node[arrow style mul] (x) {$a_{i1}\times b_{1j}$} (B-1-3); \draw[<->,red](A-3-3) to[in=180,out=90] node[arrow style mul] (y) {$a_{ik}\times b_{kj}$}(B-3-3); \draw[<->,red](A-3-5) to[in=180,out=90] node[arrow style mul] (z) {$a_{ip}\times b_{pj}$}(B-5-3); \draw[red,->] (x) to node[arrow style plus] {$+\raisebox{.5ex}{\ldots}+$} (y)% to node[arrow style plus] {$+\raisebox{.5ex}{\ldots}+$} (z); % % to (C-3-3.north west); \draw[->,red,decorate,decoration=zigzag] (z) -- (C-3-3.north west); \end{tikzpicture} \end{document}
|
@rnivelle Les formules de politesse et les signatures sont à éviter : celle(s) de votre contribution a (ont) été supprimée(s).