|
Si j'ai la longueur de l'hypoténuse et celle d'un côté, comment puis-je construire un triangle rectangle en TikZ ? Je suis à peu près certain que c'est possible mais je n'y réussis pas. J'ai regardé du côté de |
|
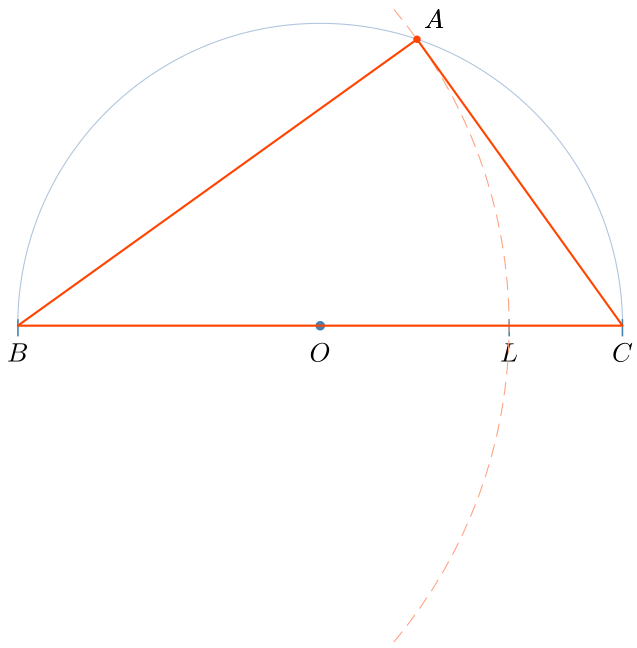
En TikZ, je ne sais pas. Mais en \documentclass[a4paper,10pt, svgnames, border=3pt]{standalone} \usepackage[utf8]{inputenc} \usepackage[T1]{fontenc}% \usepackage{lmodern} \usepackage{pst-eucl, auto-pst-pdf} \begin{document} \begin{pspicture*}(-5,-5)(5,5) \psset{dimen=middle, linejoin=1} \pstGeonode[PointSymbol=none, PosAngle=-90](-4,0){B}(0,0){O}(4,0){C}(2.5,0){L} \pstArcOAB[linewidth=0.4pt, linecolor=LightSteelBlue]{O}{C}{B} \psdots[dotstyle=|, dotsize=5pt, linecolor=SteelBlue](B)(C)(L) \psdot[linecolor=SteelBlue, linecolor=SteelBlue](O) \pstInterCC[PosAngleA=50, RadiusA=\pstDistAB{B}{L}, CodeFigA=true, CodeFigAarc=false, CodeFigColor=OrangeRed! 50, linewidth=0.4pt, linecolor=OrangeRed]{B}{}{O}{B}{A}{} \pspolygon[linecolor=OrangeRed](B)(A)(C) \end{pspicture*} \end{document} ![alt text][1]
|
|
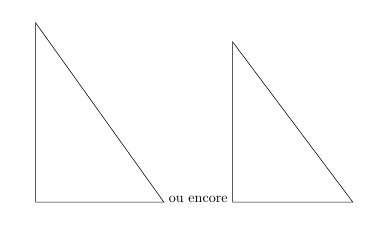
Solution 1. Une solution avec TikZ basée sur \begin{tikzpicture} \coordinate (A) at (0,0); \coordinate (B) at (3.2,0); \pgfmathparse{sqrt((5.5)^2-(3.2)^2)} \coordinate (C) at (0,\pgfmathresult); \draw (A)--(B)--(C)--cycle; \end{tikzpicture} ou (plus courte, mais moins élégante !) : \begin{tikzpicture} \pgfmathparse{sqrt((5)^2-(3)^2)} \edef\triangle{\pgfmathresult} \draw (0,0)--(3,0)--(0,\triangle)--cycle; \end{tikzpicture} ECM \documentclass{article} \usepackage{tikz} \begin{document} \begin{tikzpicture} \coordinate (A) at (0,0); \coordinate (B) at (3.2,0); \pgfmathparse{sqrt((5.5)^2-(3.2)^2)} \coordinate (C) at (0,\pgfmathresult); \draw (A)--(B)--(C)--cycle; \end{tikzpicture} ou encore \begin{tikzpicture} \pgfmathparse{sqrt((5)^2-(3)^2)} \edef\triangle{\pgfmathresult} \draw (0,0)--(3,0)--(0,\triangle)--cycle; \end{tikzpicture} \end{document}
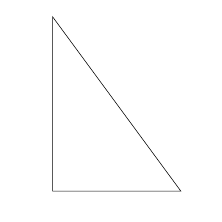
Solution 2. Une autre solution (plus élégante). Voir section \documentclass{article} \usepackage{tikz} \usetikzlibrary{calc} \begin{document} \begin{tikzpicture} \draw (0,0)--(3.2,0)--($sqrt((5.4)^2-(3.2)^2)*(0,1)$)--cycle; \end{tikzpicture} \end{document}
4
Pour insérer un calcul dans une coordonnée (lorsqu'il contient des parenthèses), il suffit de l'entourer d'accolades. Ici, la solution 2 deviendrait: |
|
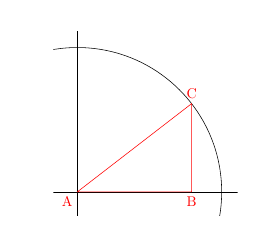
1 - Malgré la très belle introduction à pstricks de Jean-Pierre Casteleyn, lors du stage LaTeX de Dunkerque, je n'utilise pas 2 - Il s'agissait pour moi de calculer la position des sommets du triangle à partir de la longueur de l'hypoténuse et de celle d'un côté. La solution proposée par touhami ne répondait pas à cette demande, mais elle m'a appris à utiliser les fonctions \documentclass{article} \usepackage[utf8]{inputenc} \usepackage[T1]{fontenc} \usepackage{tikz} \usetikzlibrary{calc} \begin{document} \thispagestyle{empty} \begin{tikzpicture}[x = 1 mm, y = 1 mm, scale = 2] \clip (-3,-3) rectangle (20,20); % the axes \draw (0, -20) -- (0, 20); \draw (-20, 0) -- (30, 0); % the beam \draw (0,0) circle [radius=18mm]; % from texnique % Hypotenuse = radius = 18 % Opposite = half plate = 11 \coordinate (A) at (0,0); \pgfmathparse{asin(11/18)} \coordinate (B) at (\pgfmathresult:18 |- 0,0); \coordinate (C) at (\pgfmathresult:18); \draw[red] (A) node[anchor=north east] {A}-- (B) node[anchor=north] {B} -- (C) node[anchor=south] {C} --cycle; \end{tikzpicture} \end{document}
J'ai calculé la position de C à partir de l'angle en A, que j'ai déterminé en divisant la longueur du côté opposé par celle de l'hypoténuse et en appliquant la fonction arc sinus au résultat. J'ai ensuite déterminé la position du point B, qui se trouve à l'intersection ( J'ai donc déterminé la position des points B & C. Je puis donc continuer mon travail. Vive texnique.fr et sa communauté ! 1
@Pathe La solution proposée par touhami ne répondait pas à cette demande. AMHA ce n'est pas vrai. On peut résoudre un exercice de mathématiques par des méthodes différentes. Ici j'ai choisi la méthode qui m'apparis simple. :-) Vous utilisez deux points ( Mais je suis bien d'accord avec vous, on peut résoudre un exercice par plusieurs méthodes. Ce fil le montre, avec vos différentes propositions en TikZ et celle de Bernard en 3
Dans 99% des cas, en TikZ, |