|
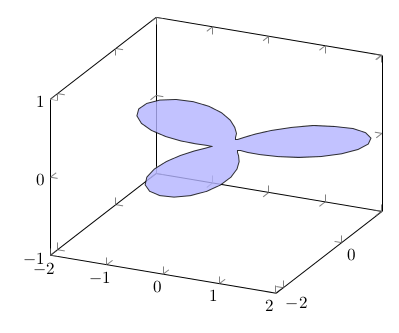
J'essaie de reproduire la figure ci-dessous à l'aide de
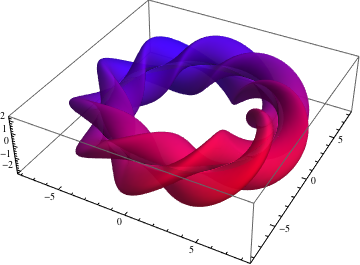
J'ai vu une explication sur mathematica stackexchange. Elle va me servir d'exemple : je vais procéder de même. Ainsi vais-je tout d'abord dessiner une coupe de la figure, puis visser celle-ci en suivant le périmètre d'un cercle. La vue en coupe est obtenue grâce au code suivant : \documentclass[border=10pt]{standalone} \usepackage{pgfplots} \usepgfplotslibrary{polar} \begin{document} \begin{tikzpicture} \begin{polaraxis} \addplot[mark=none, domain=0:360, samples=100] {sin(3*x) + 1.25}; \end{polaraxis} \end{tikzpicture} \end{document}
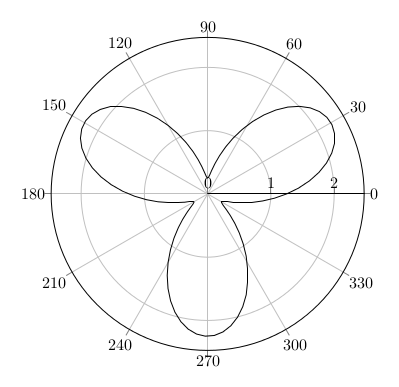
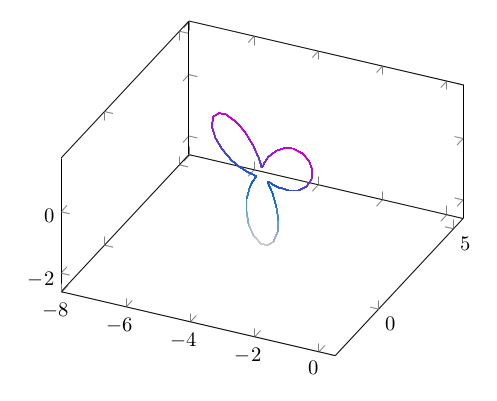
Puis je donne de celle-ci une vue en trois dimensions. Je colore ma figure pour plus de lisibilité. Par souci de simplification, je place la figure au niveau 0. Il est toujours possible de modifier cela ou de changer le point de vue. \documentclass[border=10pt]{standalone} \usepackage{pgfplots} \begin{document} \begin{tikzpicture} \begin{axis} \addplot3 [domain=0:360, samples=60, fill=blue!30, opacity=0.8] ( {cos(x)*(sin(3*x) + 1.25)}, {sin(x)*(sin(3*x) + 1.25)}, 0 ); \end{axis} \end{tikzpicture} \end{document}
Il ne nous reste plus qu'à faire tourner la figure par rapport à son centre,
pendant que celui-ci décrit un cercle selon un axe perpendiculaire au plan dans
lequel s'inscrit la figure. On trouvera sur
TeX stackexchange
un premier exemple de rotation sur l'axe Z, obtenu grâce à la fonction
Outre le fil consacré à mathematica cité plus haut, on peut s'inspirer de la documentation dudit logiciel. Car la question demeure : comment réaliser cette figure avec PS : cette question est la traduction de celle-ci, posée sur le forum germanophone texwelt.de. |
|
Il s'agit de réaliser une sorte de tore ouvert vissé, en fait. On peut s'inspirer de ce fil sur TeX stackexchange, intitulé Comment dessiner un tore ? On y lira qu'un tore peut par exemple être obtenu par l'équation : x(t,s) = (2+cos(t))*cos(s+pi/2) y(t,s) = (2+cos(t))*sin(s+pi/2) z(t,s) = sin(t) dont \documentclass[border=10pt]{standalone} \usepackage{pgfplots} \pgfplotsset{compat=1.8} \pgfplotsset{trig format plots=rad} \begin{document} \begin{tikzpicture} \begin{axis} \addplot3[surf, colormap/cool, samples=20, domain=0:2*pi,y domain=0:2*pi, z buffer=sort] ({(2+cos(x))*cos(y+pi/2)}, {(2+cos(x))*sin(y+pi/2)}, {sin(x)}); \end{axis} \end{tikzpicture} \end{document} Il s'agit de dessiner en 3D la figure 2D obtenue par les équations suivantes : x(t) = sin(3t)cos(t) y(t) = sin(3t)sin(t) Un peu de gamberge nous amène à : x(t,s) = (4+(sin(3*(t))+1.25)*cos(t))*cos(s) y(t,s) = (4+(sin(3*(t))+1.25)*cos(t))*sin(s) z(t,s) = ((sin(3*(t))+1.25)*sin(t)) Ce qui nous donne, pour une valeur définie de
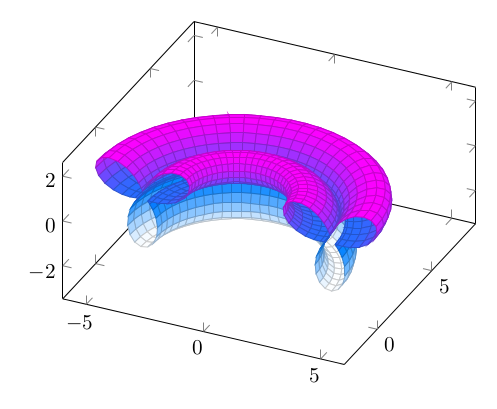
\documentclass[border=10pt]{standalone} \usepackage{pgfplots} \pgfplotsset{compat=1.11} \begin{document} \begin{tikzpicture} \begin{axis}[axis equal] \addplot3[ surf, samples=50, samples y=30, colormap/cool, domain=0:360, y domain=0:180, z buffer=sort, ] ({4+(sin(3*(x))+1.25)*cos(x))*cos(160}, {4+(sin(3*(x))+1.25)*cos(x))*sin(160}, {(sin(3*(x))+1.25)*sin(x)}); \end{axis} \end{tikzpicture} \end{document} À partir de là, on peut faire varier
\documentclass[border=10pt]{standalone} \usepackage{pgfplots} \pgfplotsset{compat=1.11} \begin{document} \begin{tikzpicture} \begin{axis}[axis equal] \addplot3[ surf, samples=50, samples y=30, colormap/cool, domain=0:360, y domain=0:180, z buffer=sort, ] ({4+(sin(3*(x))+1.25)*cos(x))*cos(y}, {4+(sin(3*(x))+1.25)*cos(x))*sin(y}, {(sin(3*(x))+1.25)*sin(x)}); \end{axis} \end{tikzpicture} \end{document} Avec
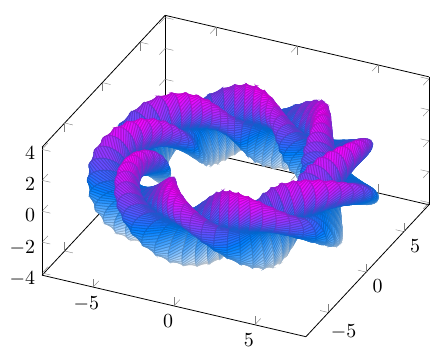
Fort bien, mais de vissage, point. On ajoute un multiple de y : On obtient le code suivant : % Avec LuaLaTeX en raison du calcul difficile \RequirePackage{luatex85}% solution temporaire pour standalone avec LuaTeX \documentclass[border=10pt]{standalone} \usepackage{pgfplots} \begin{document} \begin{tikzpicture} \begin{axis}[axis equal] \addplot3[ surf, domain = 0:360, y domain = 0:360, samples = 100, samples y = 70, z buffer = sort, colormap/cool, ] ( {(6+(sin(3*(x+3*y))+1.25)*cos(x))*cos(y)}, {(6+(sin(3*(x+3*y))+1.25)*cos(x))*sin(y)}, {((sin(3*(x+3*y))+1.25)*sin(x))} ); \end{axis} \end{tikzpicture} \end{document}
Supplément:
% Avec LuaLaTeX \RequirePackage{luatex85}% solution temporaire pour standalone avec LuaTeX \documentclass{standalone} \usepackage{pgfplots} \usetikzlibrary{backgrounds} \begin{document} \begin{tikzpicture} \begin{axis}[axis equal, hide axis, /tikz/background rectangle/.style = { left color = black, right color = black!20, shading angle = 135, }, show background rectangle ] \addplot3[ surf, shader = flat, miter limit = 1, domain = 0:360, y domain = 0:360, samples = 100, samples y = 70, z buffer = sort, colormap/hot2, ] ( {(6+(sin(3*(x+3*y))+1.25)*cos(x))*cos(y)}, {(6+(sin(3*(x+3*y))+1.25)*cos(x))*sin(y)}, {((sin(3*(x+3*y))+1.25)*sin(x))} ); \end{axis} \end{tikzpicture} \end{document} PS : cette réponse est une adaptation de celle citée plus haut ainsi que de celle-ci avec l'aide de cmhughes. L'auteur a également publié un billet de blog (en anglais) consacré au présent fil de discussions. |


Cette question ne nécessite pas de support urgent : une solution (à but d'archive) va suivre mais sentez-vous libre de contribuer si vous le souhaitez.